Benefits of Using Fraction Equation Worksheets
Fraction equation worksheets offer numerous advantages, including building proficiency in solving equations and simplifying diverse forms. Practice with these worksheets helps students visualize and understand the solution process. They also make learning more engaging.
Proficiency in Solving Equations
Consistent practice with fraction equation worksheets is crucial for developing proficiency in solving various types of equations. These worksheets provide a structured approach, enabling students to hone their skills in isolating variables and applying fundamental algebraic principles. The repeated exposure to different equation structures helps in building a strong foundation. This practice will not only enhance speed and accuracy but also build confidence when dealing with equations; Such proficiency is important for further mathematical studies and real-world applications. Through dedicated practice, students learn to approach and solve equations confidently. Engaging with diverse problems enhances critical thinking and problem-solving skills, fostering a deeper understanding of algebraic concepts. Regular use of these worksheets leads to mastery.
Simplifying Various Forms of Fraction Equations
Fraction equation worksheets are instrumental in teaching students how to simplify diverse forms of fraction equations. These resources present equations with varying complexities, from one-step to multi-step, ensuring comprehensive practice. Students learn to recognize and apply appropriate simplification techniques, such as clearing fractions by multiplying by the denominator or using the lowest common denominator (LCD). This variety of problems equips students with the skills to handle equations involving mixed numbers, improper fractions, and complex algebraic expressions, building their adaptability. By working with diverse problems, students develop a systematic approach to problem-solving, thus improving their algebraic prowess. This flexibility is crucial for handling real-world problems. The ability to simplify these forms makes solving such equations more manageable.
Visualizing and Understanding the Process
Fraction equation worksheets facilitate the visualization and comprehension of the solution process. These worksheets provide a structured approach, breaking down complex equations into manageable steps, making it easier for students to grasp each operation. By working through various examples, students internalize the logical sequence required to solve equations with fractions. This repeated exposure not only builds procedural fluency but also promotes a deeper conceptual understanding. The clear format of the worksheets helps students visualize the impact of each step, enhancing their ability to anticipate the next move. This visual clarity minimizes confusion, making the process more intuitive and less intimidating. Students begin to understand the underlying principles of solving fraction equations, not just memorizing steps. They can see and understand how the manipulations affect the equation, leading to correct solutions.
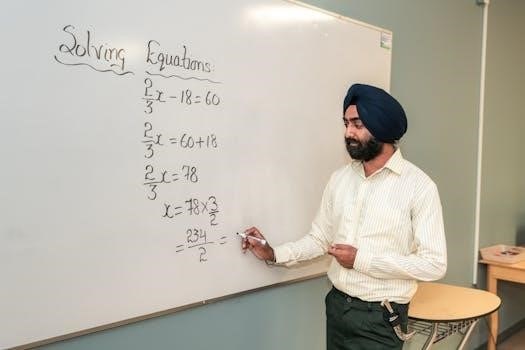
Types of Fraction Equations
Fraction equations vary in complexity, ranging from one-step to multi-step forms. They also include equations with parentheses, and literal equations. Understanding these types is crucial for solving them effectively.
One-Step Equations with Fractions
One-step equations involving fractions are the most basic type, requiring only a single operation to isolate the variable. These equations can be solved using addition, subtraction, multiplication, or division. Typically, you would perform the inverse operation on both sides of the equation to solve for the variable, for example, if the equation involves adding a fraction, then you would subtract that fraction from both sides. The goal is to have the variable by itself on one side of the equals sign. Mastery of these is essential before moving to more complex equations. Practice with these types of equations is crucial for building a solid foundation in algebra.
Two-Step Equations with Fractions
Two-step equations with fractions require two operations to isolate the variable. These equations typically involve both addition or subtraction and multiplication or division. To solve them, you first need to isolate the term with the variable by performing addition or subtraction, and then perform the inverse operation to isolate the variable. These equations build upon the skills learned in one-step equations and require an understanding of order of operations with fraction arithmetic. Careful attention to detail is required to avoid errors. Consistent practice with these equations is crucial for developing algebraic proficiency and confidence with fractions.
Multi-Step Equations with Fractions
Multi-step equations with fractions present a more complex challenge, involving several operations to solve for the variable. These problems can include combining like terms, distributing, and multiple instances of fraction arithmetic. Solving them often requires a strategic approach, including simplifying fractions first. Students must utilize their knowledge of one-step and two-step equations, as well as the order of operations, to successfully solve these more intricate problems. These equations are essential for developing higher-level algebra skills, demanding careful attention to detail and a firm grasp of fraction manipulation. The complexity of these equations makes them vital for advancing algebraic understanding.

Techniques for Solving Fraction Equations
Solving fraction equations effectively involves strategies like clearing fractions by multiplying by the denominator. Another technique is utilizing the lowest common denominator (LCD) to simplify equations before solving. These methods streamline the process.
Clearing Fractions by Multiplying by the Denominator
One effective technique for solving equations with fractions is to eliminate the fractions early in the process. This is done by multiplying each term of the equation by the denominator of the fraction involved. When there are multiple fractions, multiplying by a common denominator will clear all the fractions in a single step. This approach simplifies the equation, making it easier to solve. It transforms the equation into one with whole numbers, which are generally more straightforward to handle. This method is particularly useful when dealing with linear equations that include fractions. It’s a great way to reduce the complexity of the problem.
Using the Lowest Common Denominator (LCD)
Employing the Lowest Common Denominator (LCD) is a crucial technique for solving equations with fractions. The LCD is the smallest multiple that all denominators in the equation share. When you multiply every term in the equation by the LCD, all the fractions are eliminated, simplifying the equation. Using the LCD ensures that you’re working with the smallest possible whole numbers, which minimizes the chance of errors and keeps computations manageable. This method is especially effective when dealing with multiple fractions with different denominators. The LCD technique is a fundamental skill in algebra and simplifies the process of solving equations containing fractions.
Practice Resources for Fraction Equations
Various resources exist for practicing fraction equations, including printable worksheets that offer structured exercises. Online games also provide an engaging and interactive method to reinforce these skills, making learning enjoyable.
Printable Worksheets for Practice
Printable worksheets are a valuable resource for mastering fraction equations, providing a structured approach to learning. These worksheets feature a wide range of problems, from one-step to multi-step equations, incorporating various complexities like integers, fractions, and decimals. They offer diverse formats, including multiple-choice questions and word problems, ensuring comprehensive practice. Worksheets are available for different skill levels, allowing tailored practice. Furthermore, many sources provide free, downloadable worksheets, making them accessible for students to practice and hone their skills at their own pace. These materials often include answer keys for self-assessment.
Online Games for Engaging Practice
Online games provide an engaging alternative for practicing fraction equations, transforming a sometimes tedious task into an interactive experience. These games often incorporate elements of competition and reward, motivating students to actively participate. They typically offer varied challenges, from simple one-step equations to complex multi-step problems involving fractions, integers and decimals. Many games provide instant feedback, allowing students to correct their mistakes and improve their skills immediately. The gamified approach helps students learn through play, making the process enjoyable and reinforcing concepts through repetition and strategic thinking. Online platforms offer a variety of free games, making them easily accessible.

Advanced Fraction Equation Concepts
Advanced concepts include solving literal equations with fractions and tackling equations containing parentheses. These skills require a deeper understanding of algebraic manipulation and fraction rules, preparing students for more complex problems;
Solving Literal Equations with Fractions
Solving literal equations involving fractions extends beyond simple numerical solutions. It requires manipulating equations with variables as coefficients and constants, adding an extra layer of complexity. This skill is essential for higher-level math and science courses, where formulas are frequently rearranged. Students learn to isolate specific variables by applying the same algebraic principles used with numerical equations, but now with symbolic representations. This includes clearing fractions by multiplying by the least common denominator and strategically using inverse operations to achieve the desired variable isolation. Practicing these types of problems builds a strong foundation in algebraic manipulation and logical thinking. These equations often appear in physics and engineering.
Fraction Equations with Parentheses
Fraction equations with parentheses introduce an additional step in the solving process⁚ the distributive property. Before isolating the variable, students must correctly distribute the term outside the parentheses to each term inside. This often involves multiplying fractions by whole numbers or other fractions, requiring a solid understanding of fraction arithmetic. These equations can also combine clearing fractions with distribution, making them more challenging. Careful attention to the order of operations (PEMDAS/BODMAS) is crucial to avoid errors. Practice with these problems helps students develop the ability to tackle more complex equations and strengthens their overall algebraic skills. They teach valuable skills for more advanced algebraic equations.